位姿表示和坐标变换#
1 刚体的位姿表示#
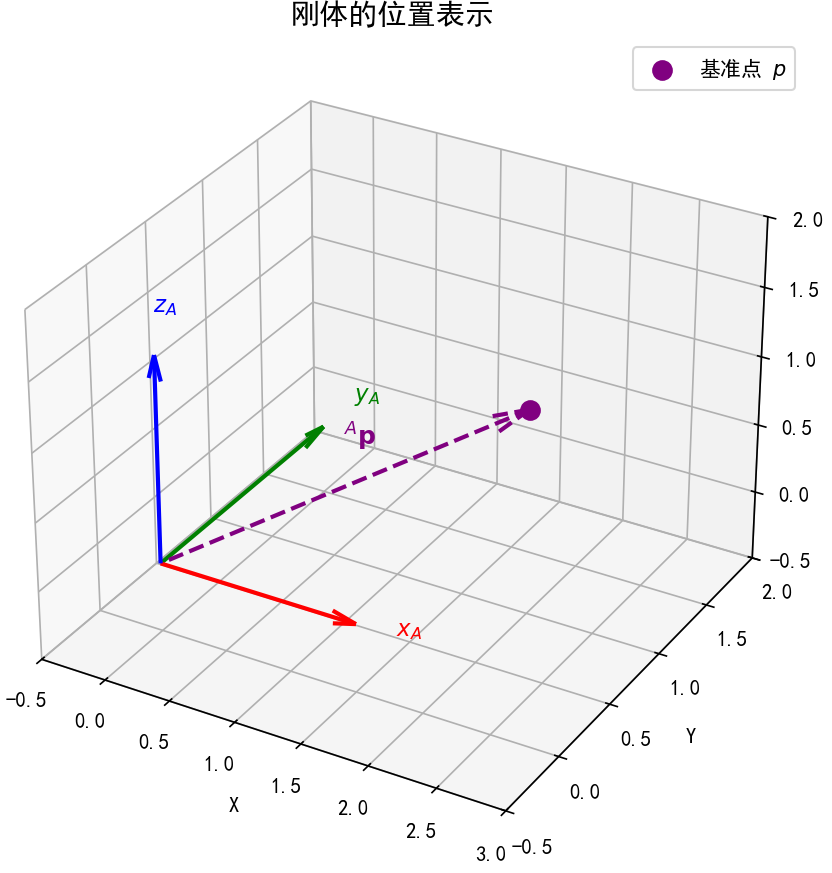
1.1 刚体的位置表示:描述 “刚体的基准点 p 在哪里”#
对于机器人等刚体,其 “位置” 需通过一个基准点 p(通常选择刚体的几何中心、质心或关键功能点,如机器人末端执行器的中心点)来定义,本质是该基准点 p 相对于参考坐标系原点的偏移关系,用位置向量即可描述。
定义:设以坐标系 \( \{A\} \) 为参考系,刚体的基准点为 \( p \)(如机器人末端中心),则 刚体相对于{A}系的位置 可表示为向量 \( {}^A \mathbf{p} \)。
符号含义:上标 \( A \) 表示 “参考坐标系为 \( \{A\} \)”,下标 \( p \) 表示 “目标是刚体的基准点 p”;
几何意义:该向量的起点为 \( \{A\} \) 系原点,终点为刚体基准点 p,唯一确定了刚体基准点 p 在 \( \{A\} \) 系中的空间位置;
数学形式:在 3D 空间中,\( {}^A \mathbf{p} \) 是 3×1 列向量,即 \( {}^A \mathbf{p} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \)(\( x、y、z \) 分别为基准点 p 在 \( \{A\} \) 系 \( x、y、z \) 轴上的坐标值);
示例:描述机器人末端执行器位置时,常以末端法兰盘中心为基准点 p,用该向量表示其在机器人基系(\( \{A\} \))中的坐标。
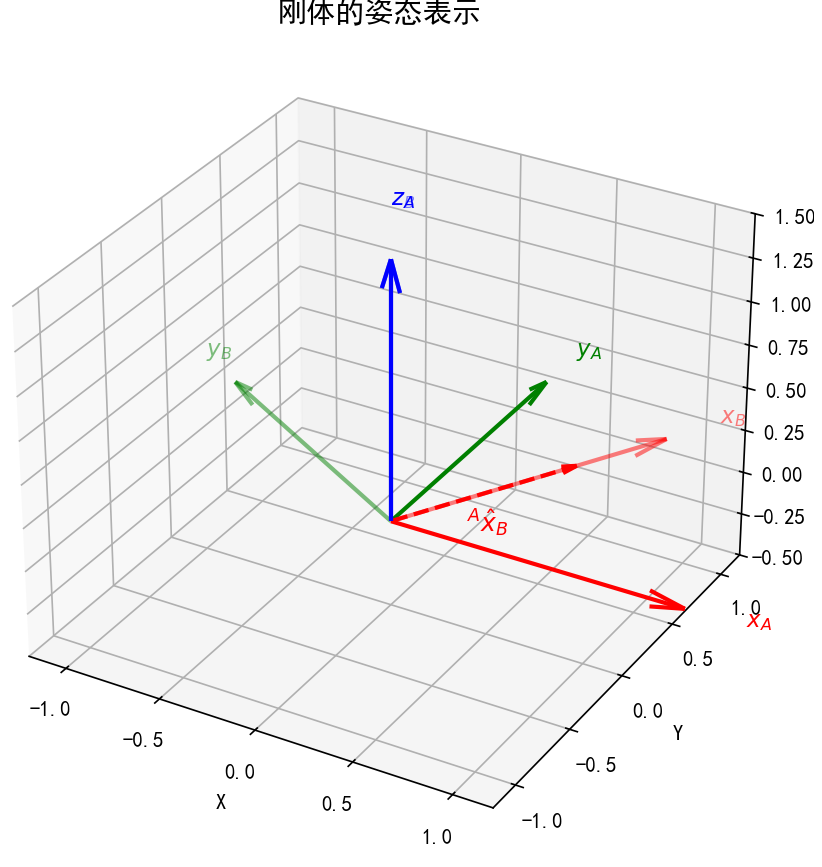
1.2 刚体的姿态表示:描述 “刚体朝哪个方向”#
刚体的 “姿态” 指其自身固连坐标系 \( \{B\} \) 相对于参考坐标系 \( \{A\} \) 的 “朝向差异”,需通过旋转矩阵定量描述 —— 本质是坐标系 \( \{B\} \) 的坐标轴相对于参考坐标系 \( \{A\} \) 坐标轴的指向关系。
定义:设刚体自身固连一个坐标系 \( \{B\} \)(称为 “刚体坐标系”,随刚体同步运动),以参考坐标系 \( \{A\} \) 为基准,则 刚体相对于{A}系的姿态 由旋转矩阵 \( {}^A R_B \) 表示。
符号含义:上标 \( A \) 表示 “参考坐标系为 \( \{A\} \)”,下标 \( B \) 表示 “目标是刚体坐标系 \( \{B\} \)”,即 “\( \{B\} \) 系相对于 \( \{A\} \) 系的姿态”;
几何意义:旋转矩阵的每一列对应刚体坐标系 \( \{B\} \) 的坐标轴在 \( \{A\} \) 系中的单位向量,即:
\( {}^A R_B = \begin{bmatrix} | & | & | \\ {}^A \hat{x}_B & {}^A \hat{y}_B & {}^A \hat{z}_B \\ | & | & | \end{bmatrix} \)
其中 \( {}^A \hat{x}_B \)、\( {}^A \hat{y}_B \)、\( {}^A \hat{z}_B \) 分别是 \( \{B\} \) 系 \( x、y、z \) 轴单位向量在 \( \{A\} \) 系中的表示,通过这三个向量可完全确定刚体的朝向(如机器人末端的 “俯仰”“偏航”“滚转” 状态);
核心特性:仅关注 “刚体的朝向”,不涉及 “刚体的位置”,是纯粹的 “姿态描述工具”;
示例:机器人抓取物体时,需通过 \( {}^A R_B \) 确保末端执行器的姿态与物体的摆放方向匹配(如水平抓取、垂直抓取)。
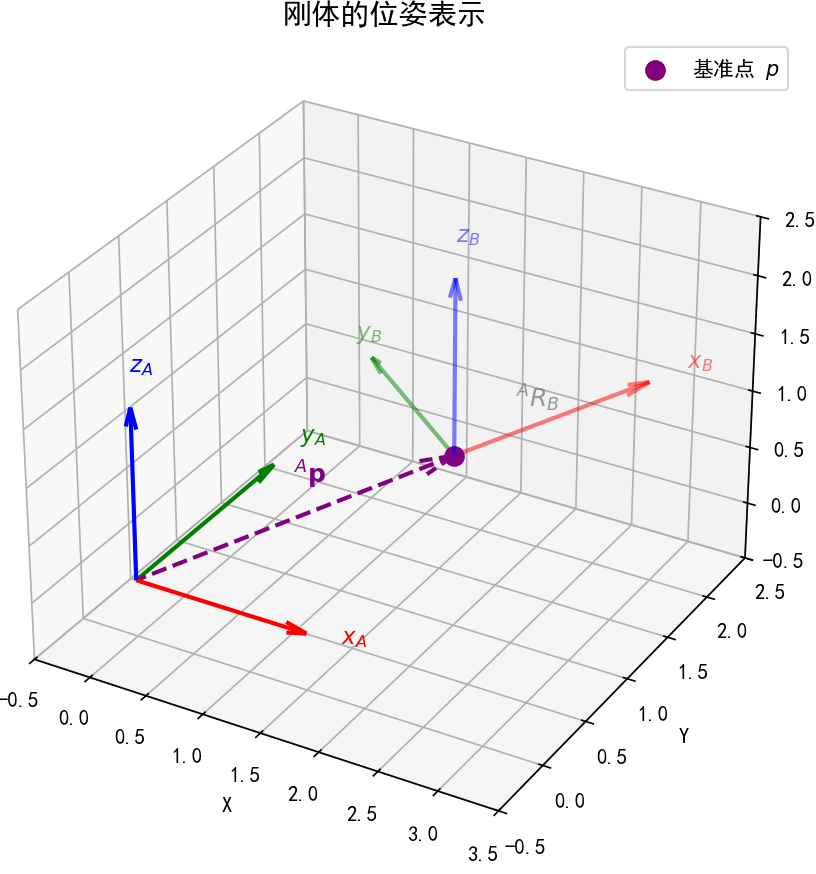
1.3 刚体的位姿表示:同时描述 “刚体在哪里” 和 “刚体朝哪个方向”#
刚体在空间中的完整状态,需同时包含 “位置”(基准点 p 的偏移)和 “姿态”(固连坐标系 \( \{B\} \) 的朝向)—— 这种综合状态称为 “位姿(Pose)”,是机器人运动规划、定位控制的核心描述量。
定义:刚体的位姿是 “位置” 与 “姿态” 的结合体,需用 “基准点 p 位置向量 + 旋转矩阵” 的组合来描述,完整刻画刚体的空间状态。
数学形式:以 \( \{A\} \) 系为参考系时,刚体的位姿可表示为 \( \{ {}^A R_B,\ {}^A \mathbf{p} \} \),其中:
\( {}^A R_B \) 描述刚体的姿态(固连坐标系 \( \{B\} \) 的朝向);
\( {}^A \mathbf{p} \) 描述刚体基准点 p 的位置(偏移);
几何意义:既通过 \( {}^A \mathbf{p} \) 确定了刚体 “在哪里”(基准点 p 的空间坐标),又通过 \( {}^A R_B \) 确定了刚体 “朝哪个方向”(固连坐标系 \( \{B\} \) 的指向),二者结合可唯一确定刚体在空间中的位置和姿态;
应用场景:
机器人运动规划:需通过位姿 \( \{ {}^A R_B,\ {}^A \mathbf{p} \} \) 定义末端执行器的目标状态(如 “移动到坐标 (0.5, 0.3, 0.8) 且姿态为水平朝上”);
刚体定位:工业机器人安装时,需通过位姿描述机器人底座相对于工作台坐标系的位置和朝向;
物体抓取:视觉引导机器人抓取时,需先识别目标物体的位姿,再调整末端执行器的位姿以匹配抓取需求。
2 坐标变换#
2.1 平移坐标变换:仅描述“原点位置差异”#
平移坐标变换的核心是:两个坐标系的姿态完全相同(坐标轴方位一致),仅原点位置不同。此时,同一点在两个坐标系中的坐标差异,仅由“原点的相对位置矢量”决定。
2.1.1 关键特征#
姿态不变:两个坐标系的x、y、z轴方向完全平行(无任何旋转)。
例如:坐标系{A}固定在桌面左上角,坐标系{B}固定在桌面右下角,两者x轴都沿桌面水平向右,y轴沿桌面竖直向前,z轴垂直桌面向上——仅原点位置不同,姿态完全一致。变换关系:设坐标系{B}的原点相对于{A}的原点的位置矢量为\( {}^A p_{B_o} \)(上标“A”表示在{A}中描述,下标“\( B_o \)”表示{B}的原点),则任一点p的坐标满足:
\( ^A \mathbf{p} = ^B \mathbf{p} + ^A \mathbf{p}_{B_o} \)
(\( ^A \mathbf{p} \)是p在{A}中的坐标,\( ^B \mathbf{p} \)是p在{B}中的坐标,\( {}^A \mathbf{p}_{B_o} \) 代表坐标系 {B} 的原点在坐标系 {A} 中的位置向量)
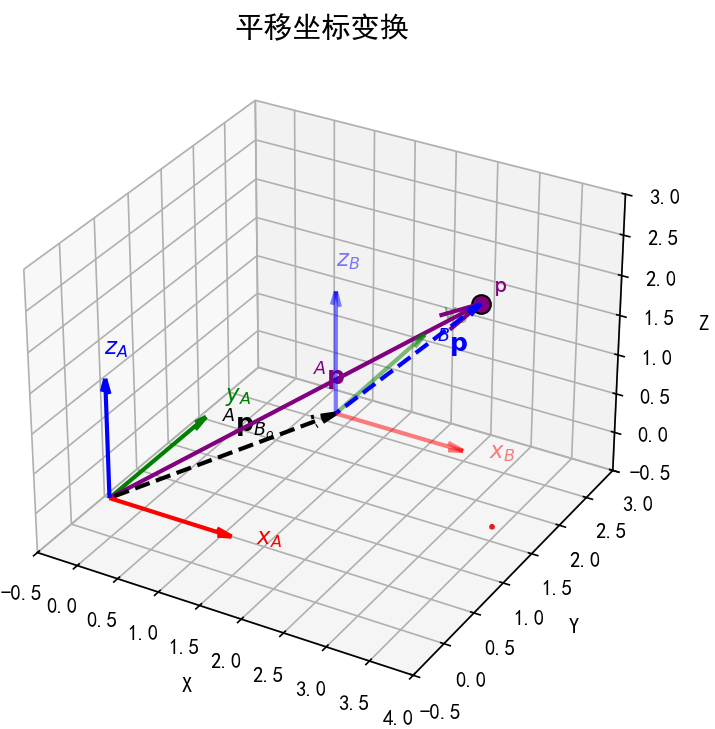
本质:仅解决“原点在哪里”的问题,不涉及“坐标轴朝哪个方向”。
2.2 旋转坐标变换:仅描述“坐标轴姿态差异”#
旋转坐标变换的核心是:两个坐标系的原点完全重合(位置相同),仅坐标轴方位不同。此时,同一点在两个坐标系中的坐标差异,由“描述姿态的旋转矩阵”决定。
2.2.1 关键特征#
位置不变:两个坐标系共享同一个原点(无任何平移)。
例如:坐标系{A}的x轴沿水平向右,坐标系{B}的原点与{A}重合,但{B}的x轴绕z轴(垂直地面)转了30°——仅姿态不同,位置完全一致。**核心工具:**旋转矩阵
旋转矩阵记为 \( {}^A R_B \),表示坐标系 {B} 相对于坐标系 {A} 的姿态。它是一个 3×3 正交矩阵,满足 \( {}^A R_B^\top = {}^A R_B^{-1} \) 这一特性。其核心作用是将在 {B} 系中描述的向量坐标,转换为在 A 系中描述的坐标,具体公式如下:
\( {}^A \mathbf{p} = {}^A R_B \cdot {}^B \mathbf{p} \)
旋转矩阵的列向量具有明确几何意义,每一列分别对应坐标系 B 的 x、y、z 轴单位向量在坐标系 {A} 中的表示,其矩阵形式可写为:
\( {}^A R_B = \begin{bmatrix} | & | & | \\ {}^A \hat{x}_B & {}^A \hat{y}_B & {}^A \hat{z}_B \\ | & | & | \end{bmatrix} \)
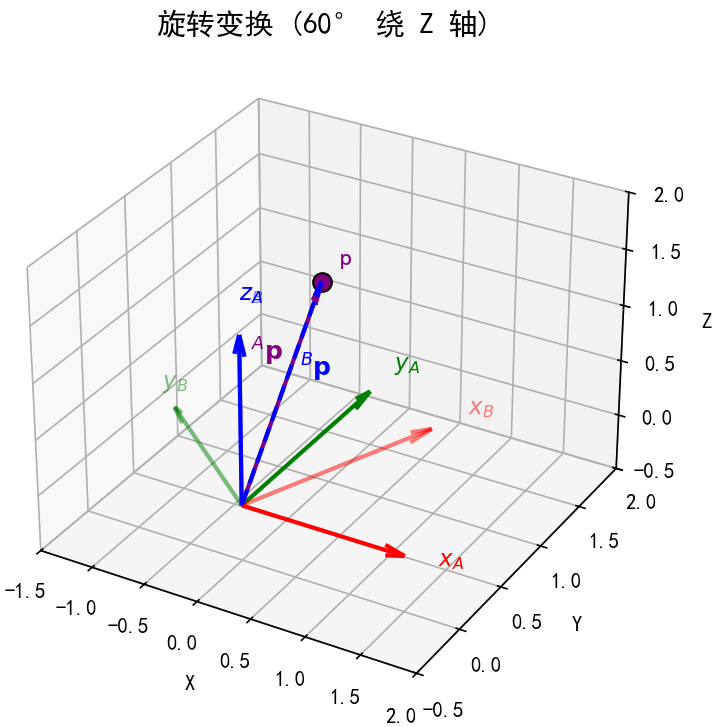
本质:仅解决“坐标轴朝哪个方向”的问题(即姿态),不涉及“原点在哪里”的位置问题。
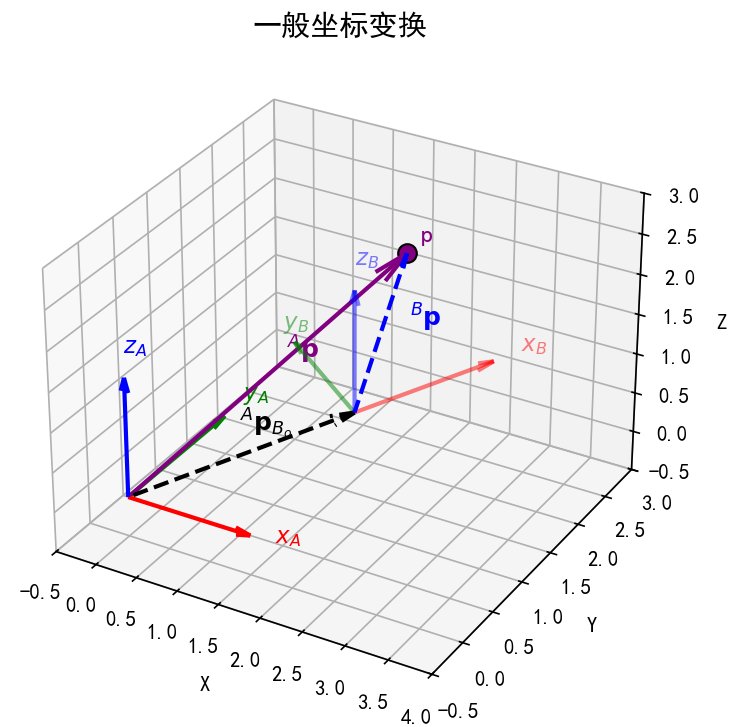
2.3 一般坐标变换公式#
当两个坐标系(如 {A} 系与 {B} 系)存在位姿差异(既含姿态差异,又含原点偏移)时,空间中点 p 在两坐标系下的坐标转换,需同时考虑 “姿态补偿”(旋转矩阵)和 “位置补偿”(原点偏移向量),具体公式如下:
\( {}^A \mathbf{p} = {}^A R_B \cdot {}^B \mathbf{p} + {}^A \mathbf{p}_{B_o} \)
公式含义:将 {B} 系中描述的点 p 坐标(\( {}^B \mathbf{p} \)),先通过 \( {}^A R_B \) 补偿姿态差异,再通过 \( {}^A \mathbf{p}_{B_o} \) 补偿原点偏移,最终得到 {A} 系中描述的点 p 坐标(\( {}^A \mathbf{p} \));
与位姿的关联:该公式本质是 “位姿 \( \{ {}^A R_B,\ {}^A \mathbf{p}_{B_o} \} \)” 在坐标转换中的具体应用,完整覆盖了 “姿态” 和 “位置” 的双重差异。